The following are main figures from the paper.
doi: xxx
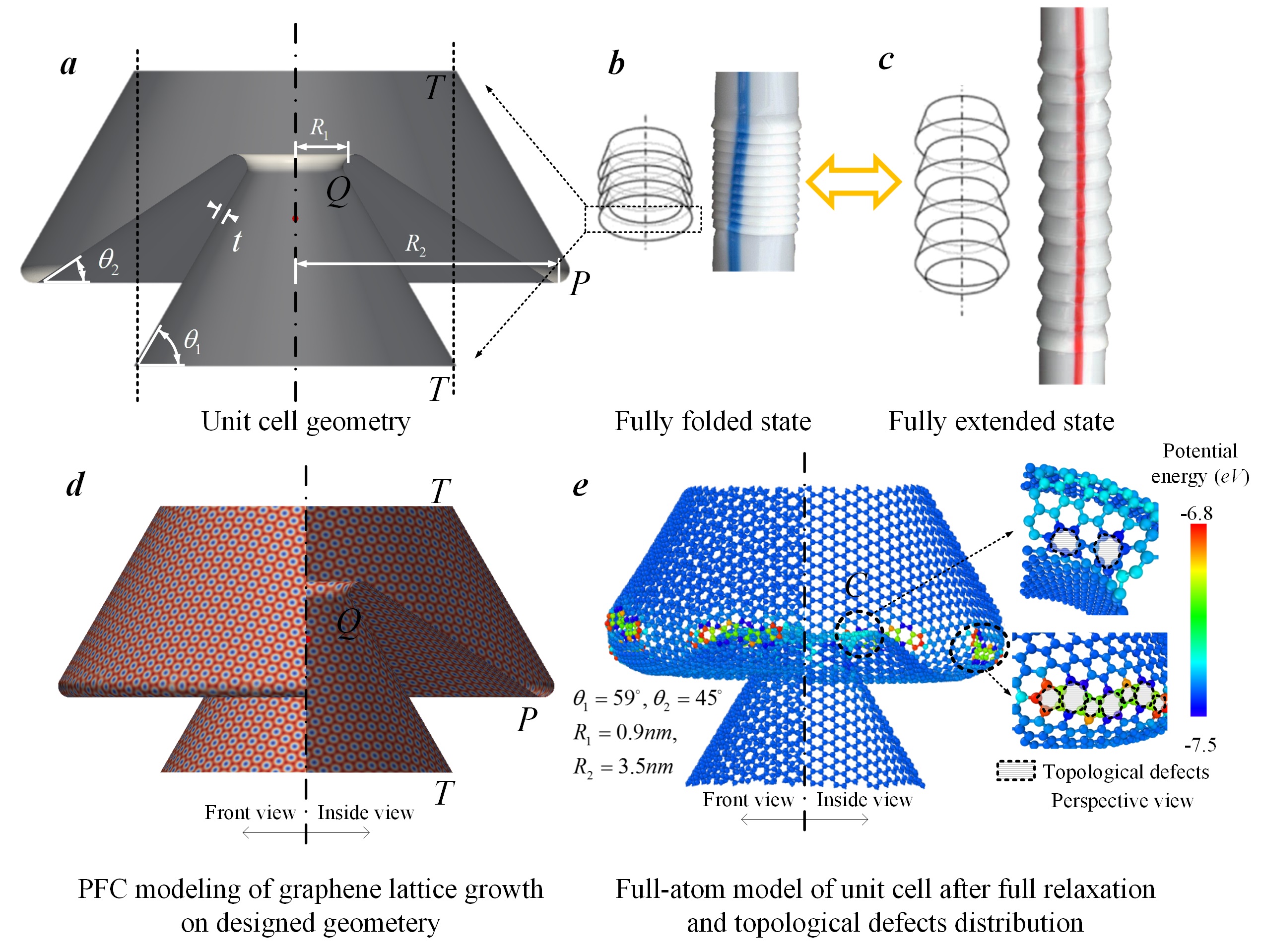Fig. 1. Unit cell of shell structure in flexible straws and its nanoscale graphene counterpart engineered via topological design. (a) Geometry of the unit cell structure in straws. (b-c) The fully folded and fully extended states of flexible straws. (d) Phase field crystal simulation of a 2D crystal sample growing on the designed shell surface. (e) The atomic structure of the graphene unit cell with straw-like geometry after MD relaxation and the topological defects distributed at the inner and outer folds.
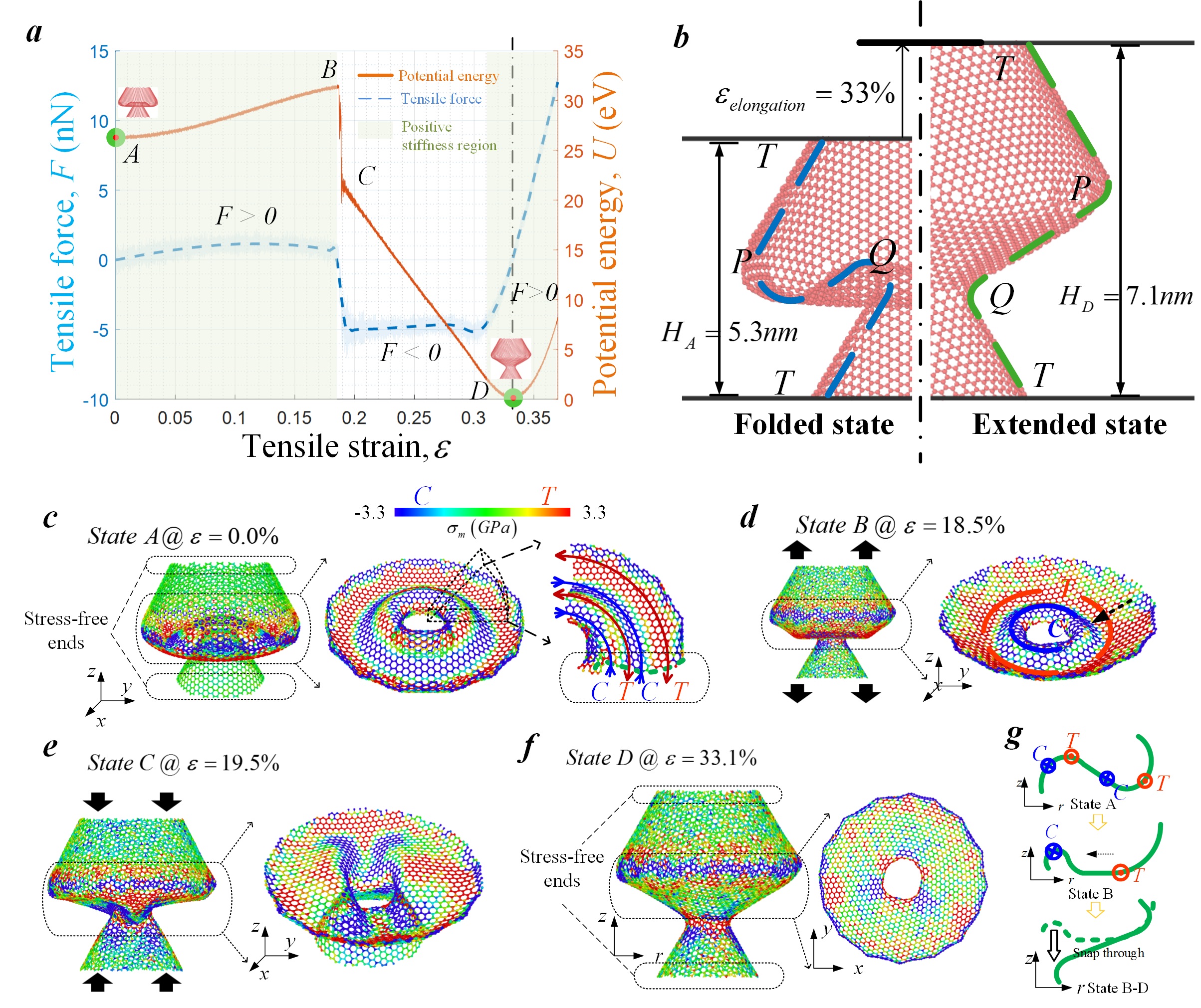Fig. 2. The two stress-free stable configurations of the unit cell and the process of a snap-through event. (a) The force-strain and potential energy-strain curves of the unit cell transforming from the folded state to the extended state. (b) Geometry of the two loading-free equilibrium configurations of the unit cell. The two halves of the unit cell are in the folded and extended states, respectively. (c-f) Snapshots of a snap-through event during a tension test in MD simulation. (g) 2D sketch of the deformation process of the inner frustrum during the snap-through process.
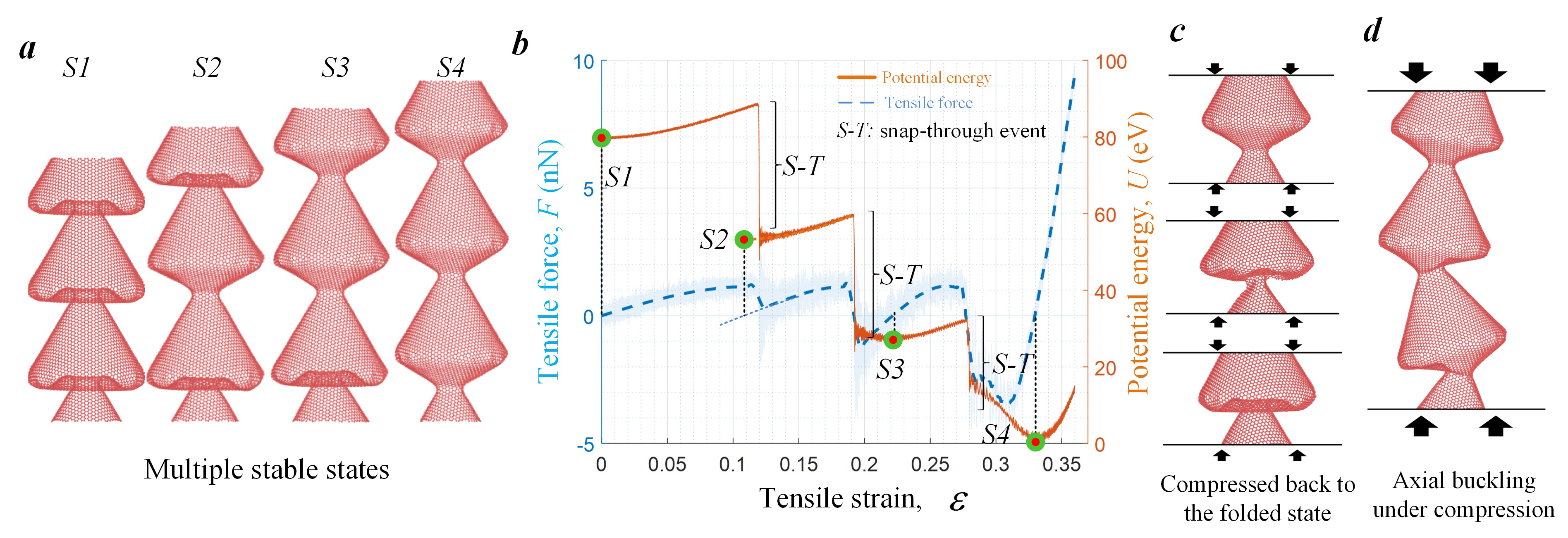Fig. 3. 1D lattice design: a straw-like CNT. (a) The four stress-free equilibrium configurations with different lengths. (b) Force-strain and potential energy-strain curves during transition from the fully folded stated to the fully extended state under tension via MD. (c) One unit cell compressed back to its folded state without suffering axial buckling. (d) Axial buckling of the SCNT with three unit cells under compression.
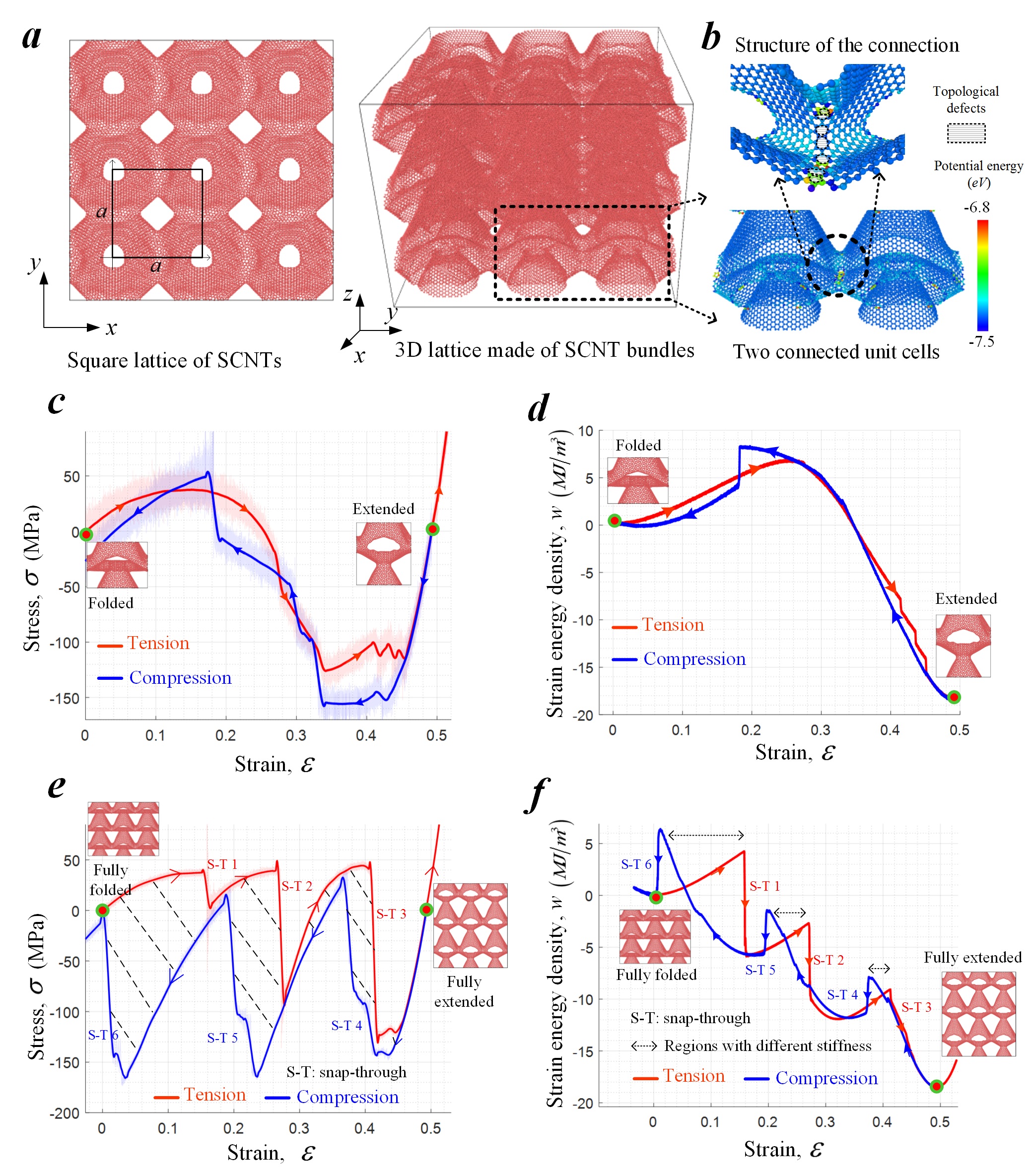Fig. 4. 3D design: 3D graphene nanolattice made of straw-like graphene unit cells. (a) The square lattice structure of SCNT bundles. (b) The covalently bonded connection between neighboring unit cells and topological defect distribution nearby. (c-d) The stress-strain and strain energy density-strain curves of a single unit cell under a tension-compression loop between the folded and extended states. (e-f) The stress-strain and strain energy density-strain curves of a 3D graphene nanolattice with 3-by-3-by-3 unit cells under a tension-compression loop between the folded and extended states.
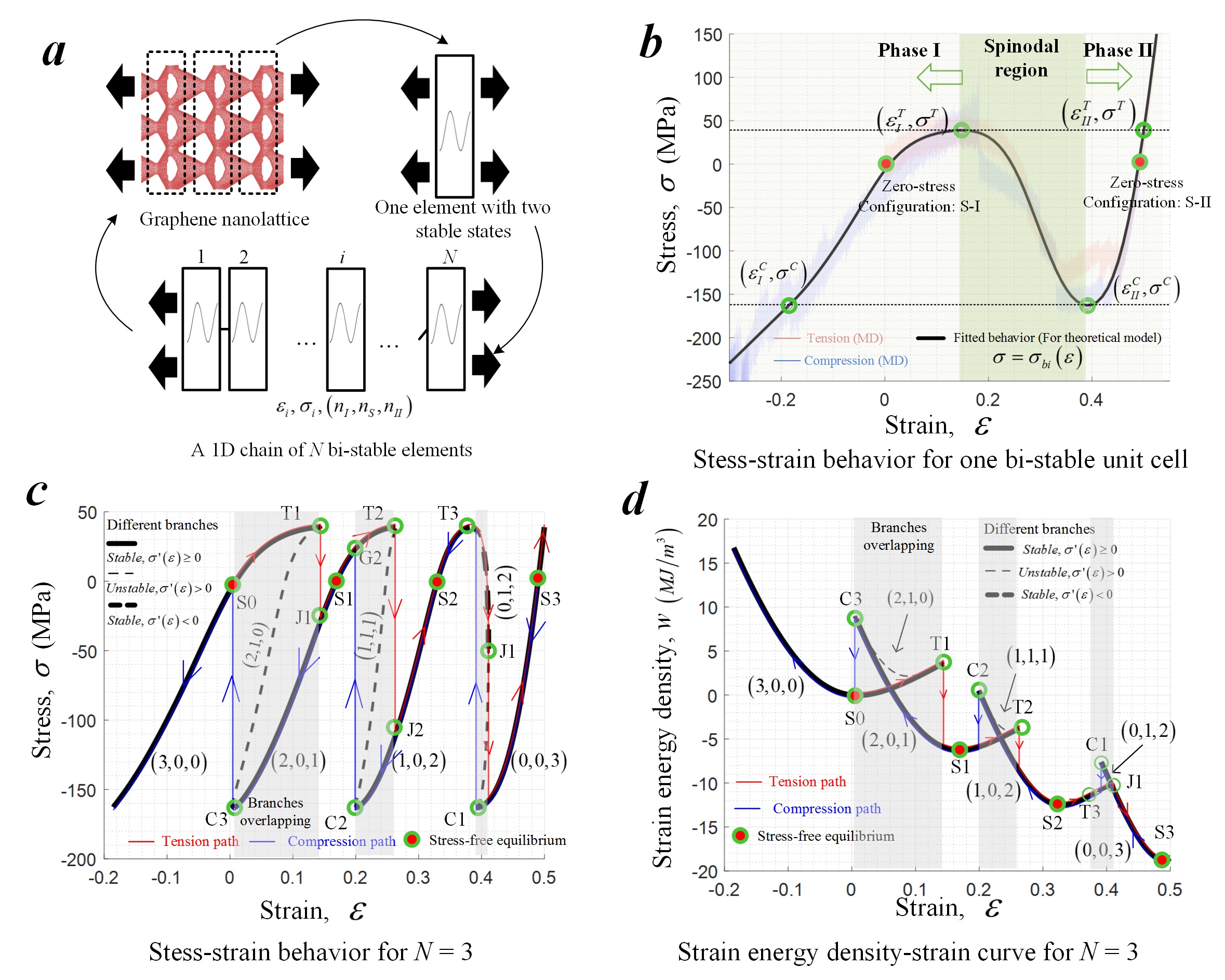Fig. 5 A theorical model of 1D chain of bi-stable elements. (a) Abstracting the graphene nanolattice with straw-like unit cell into a 1D bi-stable element chain. (b) The constitutive law of a single bi-stable element based on the MD data. (c-d) Theoretical predictions of the stable deformation branches and the paths taken under tension and compression loading on the stress-strain and strain energy density-strain curves.
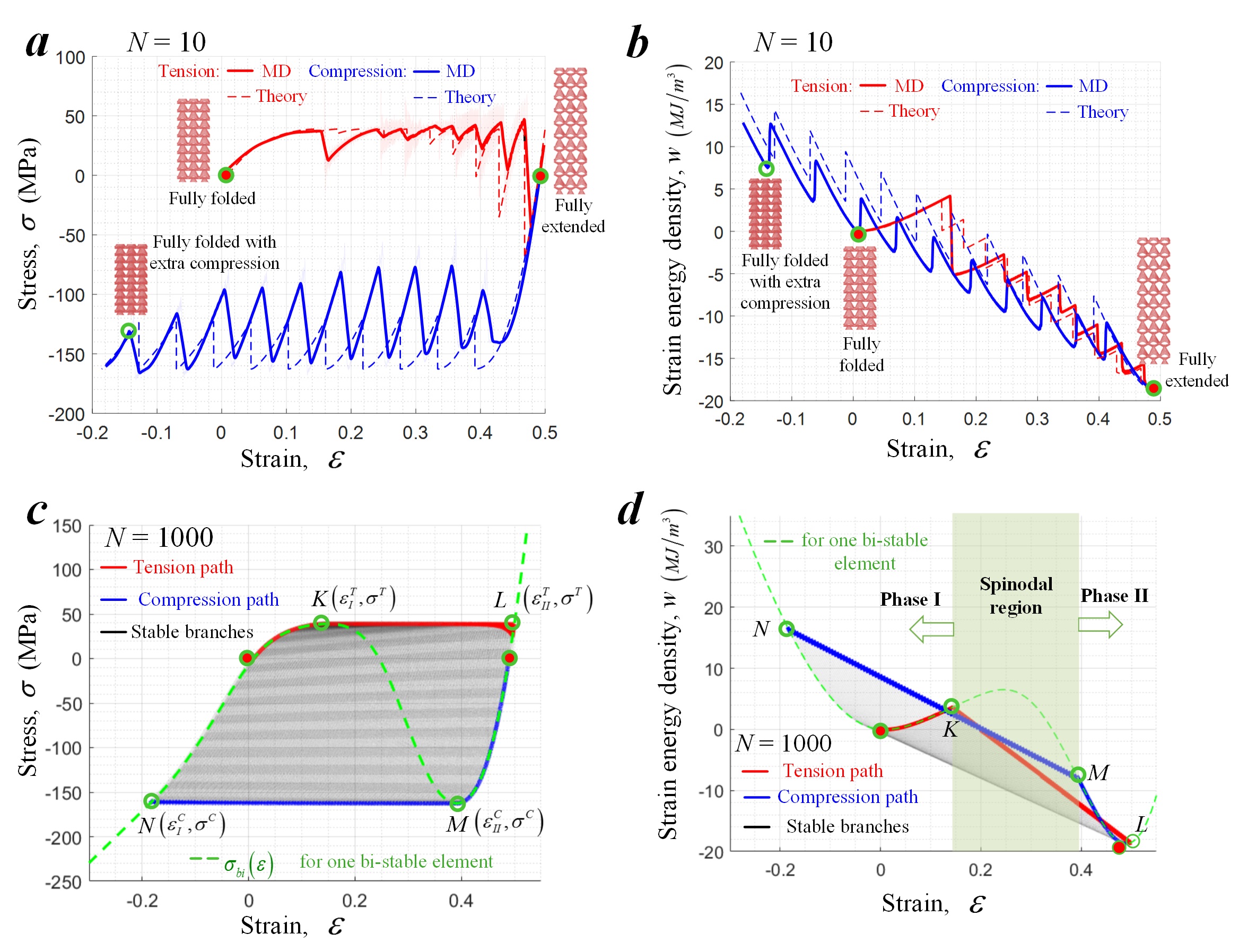Fig. 6 Validating the theoretical model and predicting the collective behavior of nanolattice with a large number of unit cells. (a-b) MD results and theoretical predictions of stress-strain and strain energy density-strain curves of the nanolattice with 10 elements along the axial direction during a tension-compression loop. (c-d) Theorical prediction of the deformation of a nanolattice with 1000 elements along the axial direction and its comparison to that of a single bi-stable element.
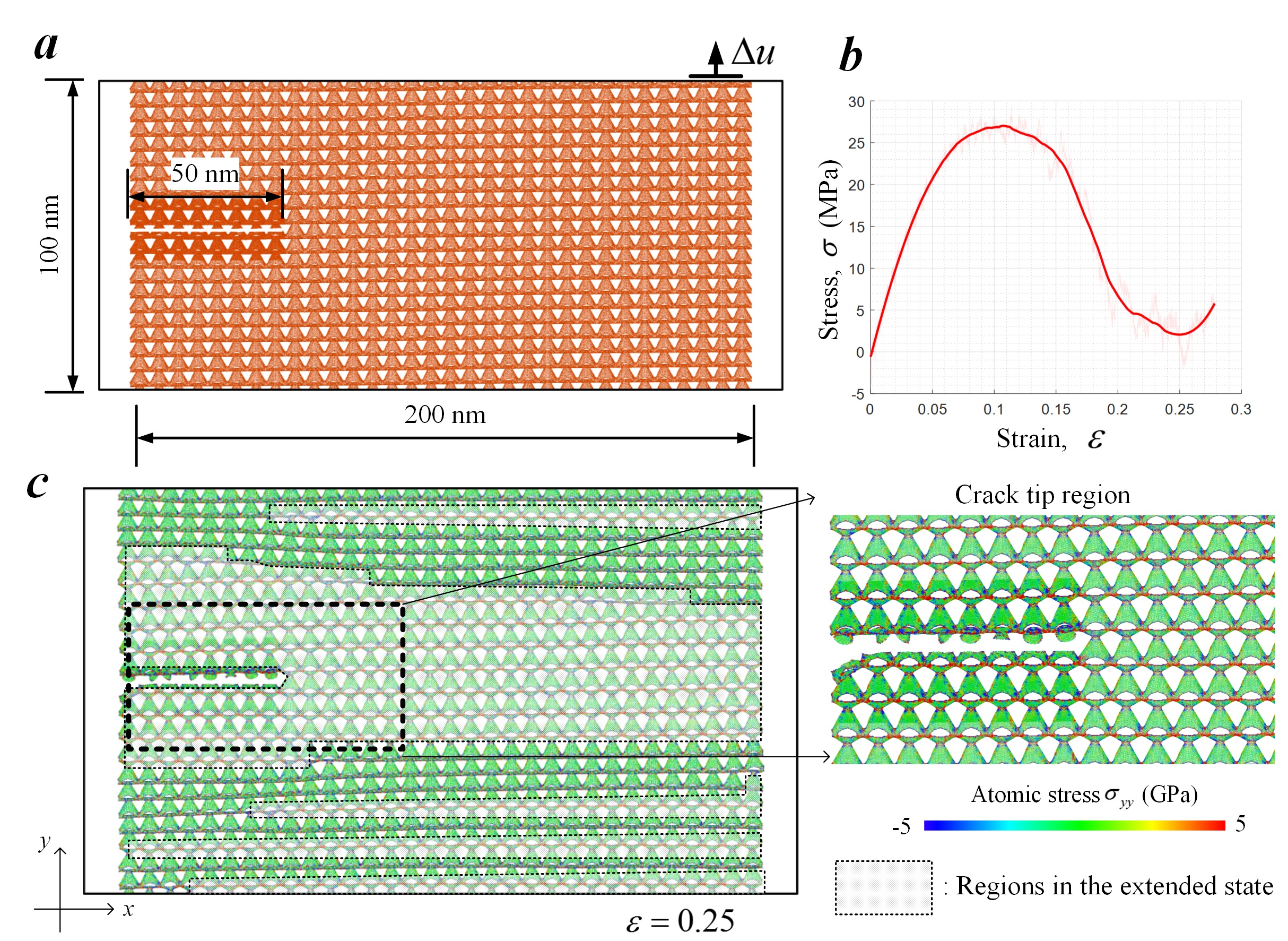Fig. 7 MD simulation of a tension test of a graphene nanolattice slab with an edge crack. (a) Geometry of the graphene nanolattice. (b) The overall stress-strain curve. (c) Crack trapping due to the band-like region around the crack tip transformed into the extended state via snap-through events.