In this section, we construct a theoretical model to explain our observation of 3D graphene nanolattice with snap-through stability and predict the collective behavior of samples with large members of unit cells.

Theoretical model: 1D bi-stable element chain

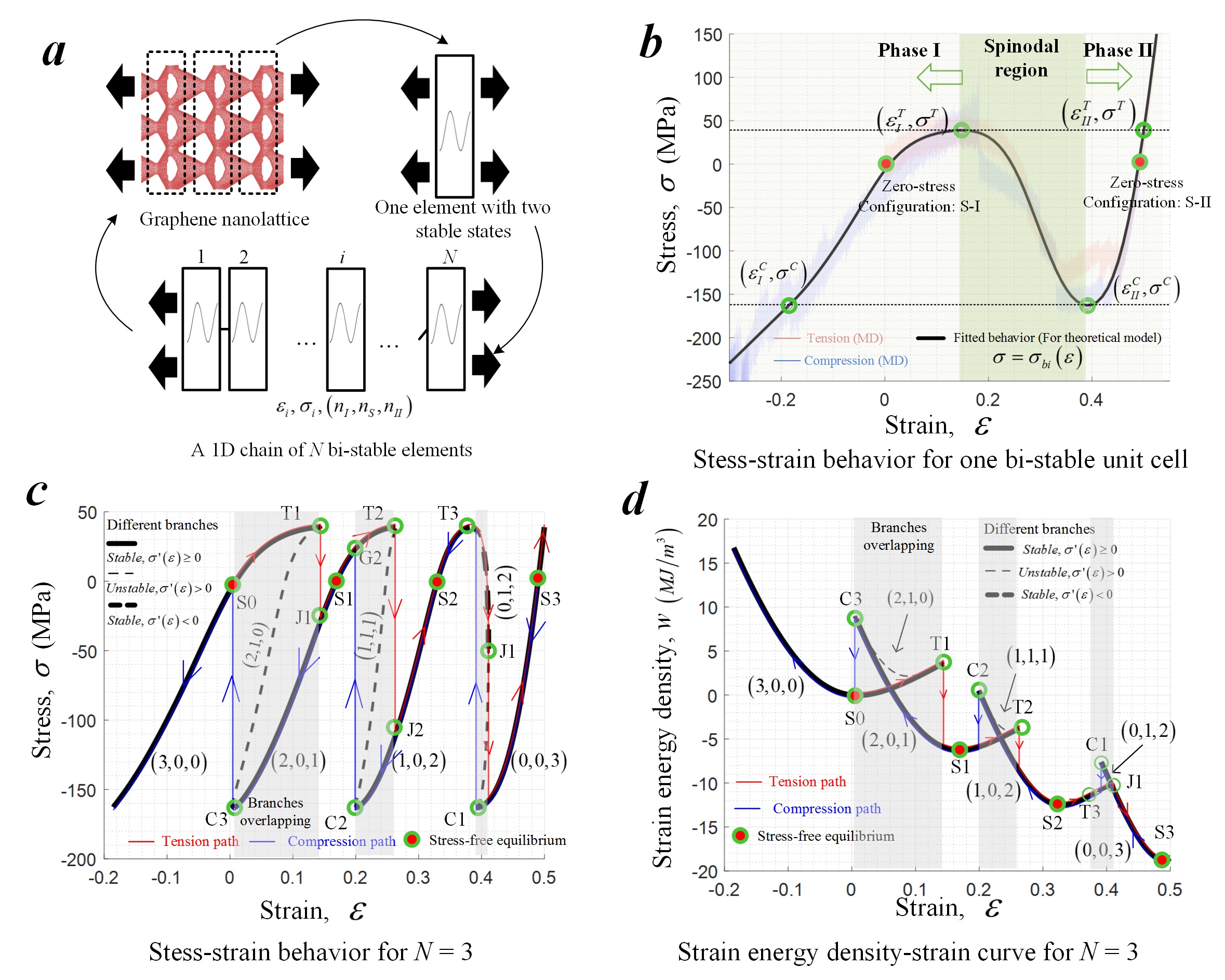Fig. 5 A theorical model of 1D chain of bi-stable elements. (a) Abstracting the graphene nanolattice with straw-like unit cell into a 1D bi-stable element chain. (b) The constitutive law of a single bi-stable element based on the MD data. (c-d) Theoretical predictions of the stable deformation branches and the paths taken under tension and compression loading on the stress-strain and strain energy density-strain curves.

We adopted a theoretical model of 1D chain of bi-stable elements to study the nanolattices (Fig. 5 a) phenomenologically.

• The unit cell is characterized by the stress-strain curve with a spinodal region and two stress-free equilibrium configurations with different lengths and stiffnesses, Phase I and II ( Fig. 5 b)
• THe unit cells are identical and connected one after another along the axial direction.
• We define the state of the system using the numbers of elements in the Phase I, II and spinodal region respectively. Different states correspond to different stress-free equilibrium configurations.

Assume the deformation process is quasi-static and over-damped. By force balance and stable equlibrium condition, we can find for a given displacement-controlled loading path,

• Multiple deforamtion branches with different system states exits.
• These branches often discontinous.
• These branches have overlapping on the strain interval.

By applying the condition of the continouity of loading strain, we can find the realized deformation path. The theortical model explains the observation of MD simulations. Specificly,

• The discontinuity of stable deformation branches results in the saw-teeth like stress-strain curves.
• The overlapping of stable deformation branches leads to the hysteresis loop in cyclic loading.

The theoretical prediction and the MD simulations show a good agreement (Fig. 6 a and b).

What happens when the lattice have a large number of unit cells?

Comparing the MD results, we noted that as the number of unit cell along the axial direction increases,

• the amplitude of stress oscillations along tension/compression paths decreases,
• the area of hysteresis loop increases. Based on this observation, it becomes interesting to predict
• the asymptotic behavior of nanolattice samples with large numbers of unit cells
• the upper bound of energy dissipation for this nanolattice design.

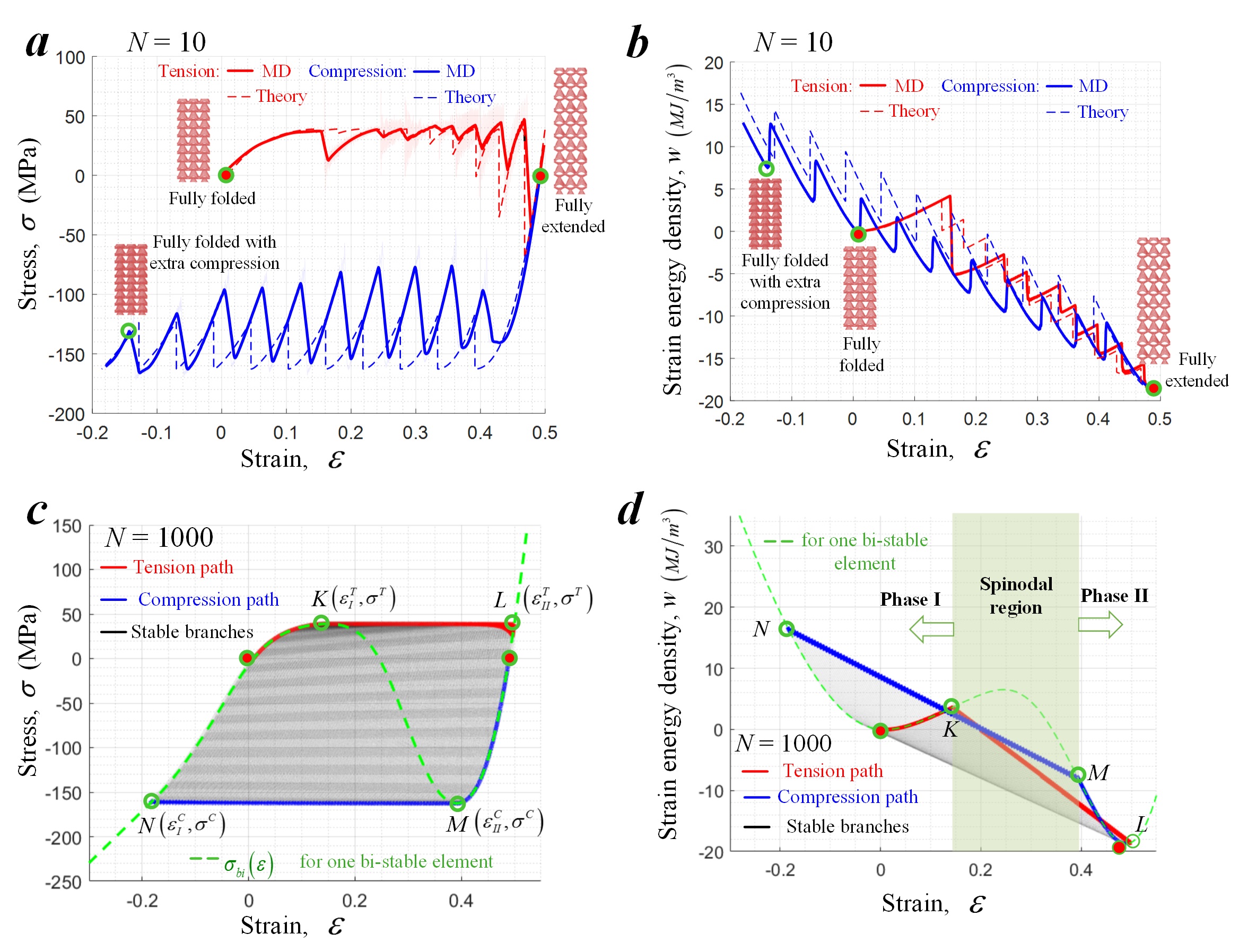Fig. 6 Validating the theoretical model and predicting the collective behavior of nanolattice with a large number of unit cells. (a-b) MD results and theoretical predictions of stress-strain and strain energy density-strain curves of the nanolattice with 10 elements along the axial direction during a tension-compression loop. (c-d) Theorical prediction of the deformation of a nanolattice with 1000 elements along the axial direction and its comparison to that of a single bi-stable element.

By keeping increasing unit cell number in the theoretical model, we observed the deformation behavior converges to (Fig. 6 c and d)

• a pseudo plastic behavior: yield and flow happens without irriversible damage,
• a finite hysteresis loop dissipating strain energy.

With these toughening mechanisms, the energy dissipation per unit mass of graphene nanolattice for a full loop between the fully folded and extended states can approach 233 kJ/kg (One order higher than the energy absorbed by carbon steel at failure, 16 kJ/kg ).

Flaw-tolerance: Loading with an edge crack

At last, we demonstrated the effect of the energy dissipation mechanisms enabled in this novel 3D graphene nanolattice on resisting crack propagation.

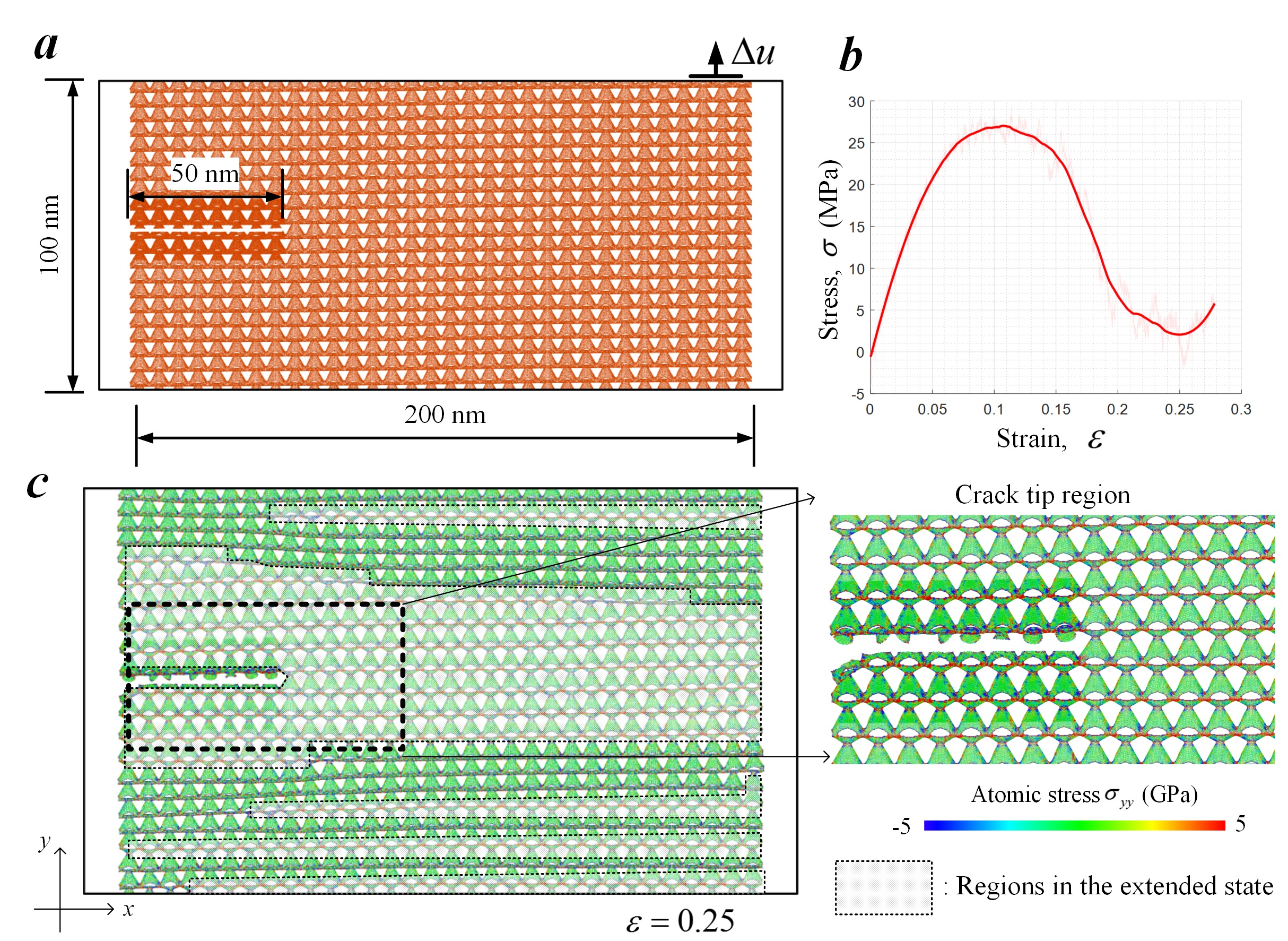Fig. 7 MD simulation of a tension test of a graphene nanolattice slab with an edge crack. (a) Geometry of the graphene nanolattice. (b) The overall stress-strain curve. (c) Crack trapping due to the band-like region around the crack tip transformed into the extended state via snap-through events.

The graphene nanolattice with snap-through instability can tolerate crack-like flaw and behave in a ductile manner within the pseudo plastic deformation region.